Title: “Design a Controller to stabilize a spacecraft’s Attitude”
Introduction
Space Exploration has always captivated the attention of all human being from women to men, from kids to adults. However, going to space is much more easier than developing the best vehicle with the right control system to reach space. In fact, in order to conduct activities in space (send human or robots, do science,…), Aerospace Engineers need to come up with innovative ideas not only to build the spacecraft but mostly to stabilize it in order to allow it to perform its mission. For example, a spacecraft designed to capture an asteroids, mining it, and bring its valuable resource back to Earth need a strong control system to be stable and perform its mission safely. In this project, I assumed that the transfer function system of a spacecraft I call “Controller” is unstable and I design (implememt) a new controller to stabilize the spacecraft.
Materials and methods
I use the Control package available in the library. Other than that I created all the rest of the data by myself. I firstly assumed a chosen transfer function system of the spacecraft I called “Controller” and tried to see if that controller could stabilize the spacecraft by ploting its step response curve. After being sure that the system is unstable with that controller by looking at the poles of the system and its step response curve, I designed a controller I called “Controller2” with some parameters I choose to make sure that it can stabilize the system of the spacecraft. I ploted the step response of the controller I designed to show that it can stabilize the system.
#Load any required packages in a code chunk (you may need to install some packages):
library(control)##
## Attaching package: 'control'## The following object is masked from 'package:stats':
##
## step## The following object is masked from 'package:base':
##
## appendDefinition of Transfer Function
A transfer function is a frequency domain, i.e. the ratio of the output to the input of the control system.
Download and clean all required data (1)
#Example of Transfer Function
a <- 10; b <- 7; k <- 3
TF("1/(a*s^2 + b *s + k)")##
## y1:
## 1
## - - - - - - - - - - -
## 10 s^2 + 7 s + 3
##
##
## Transfer Function: Continuous time modelSome transfer function are able to stabilize the system of a spacecraft without the need of designing or implementing a controller but depending on diverse factors such as forces acting on the sapcecraft, gravity torques,…the transfer function only might not be able to stabilize the spacecraft. So it is always better to test its stability depending on the mission we want to perform.
Download and clean all required data (2)
e <- 0.000003;
m <- 0.000003;
p <- 0.03;
d <- 4;
w <- 0.000003;
Controller <- TF("p/(s*((e*s + m)*(w*s + d) + p^2))")
time <- seq(0,0.5,0.0010)Results
stepplot(Controller, t = time)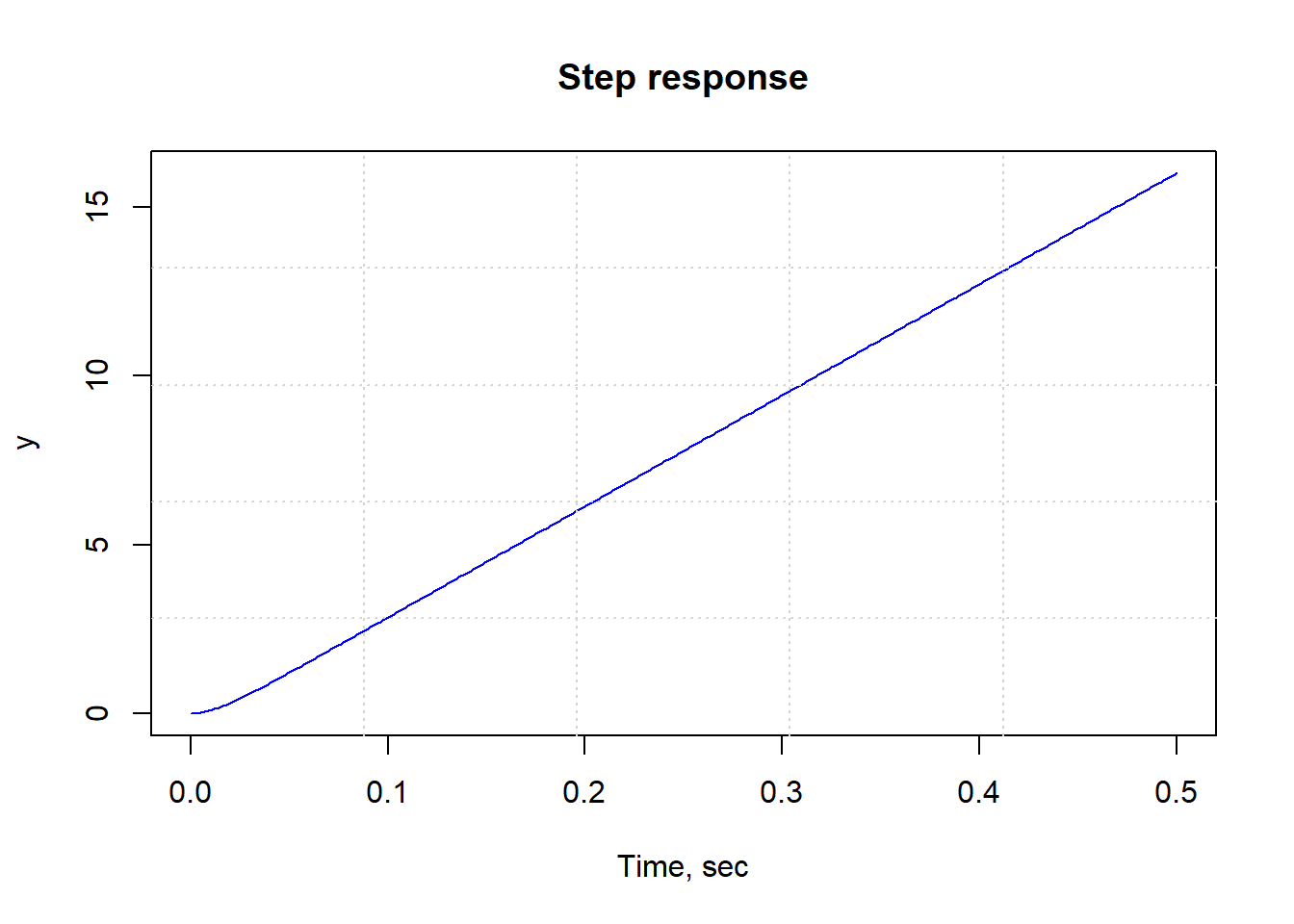
#Is the system Stable?
From the plot of the system’s step response, it is clear that the system is unstable. The Stability of the system can also be determined by looking at the poles of the system.
pole(Controller)## [,1]
## [1,] 0.000000e+00
## [2,] -1.333258e+06
## [3,] -7.600428e+01One of the poles of the open-loop transfer function is on the imaginary axis and the other two poles are in the left half of the complex s-plane. So the system is not stable.
Since the system is not stable, we need to add a feedback controller and check the closed-loop step response of the system to see if it is stable or not.
#Closed-Loop Response of the Controller
Controller2<- feedback(Controller, 1)
print(Controller2)##
## y1:
## 0.03
## - - - - - - - - - - - - - - - - - - - - - - - - - - -
## 9e-12 s^3 + 1.200001e-05 s^2 + 0.000912 s + 0.03
##
##
## Transfer Function: Continuous time model#Plot
stepplot(Controller2, t = time)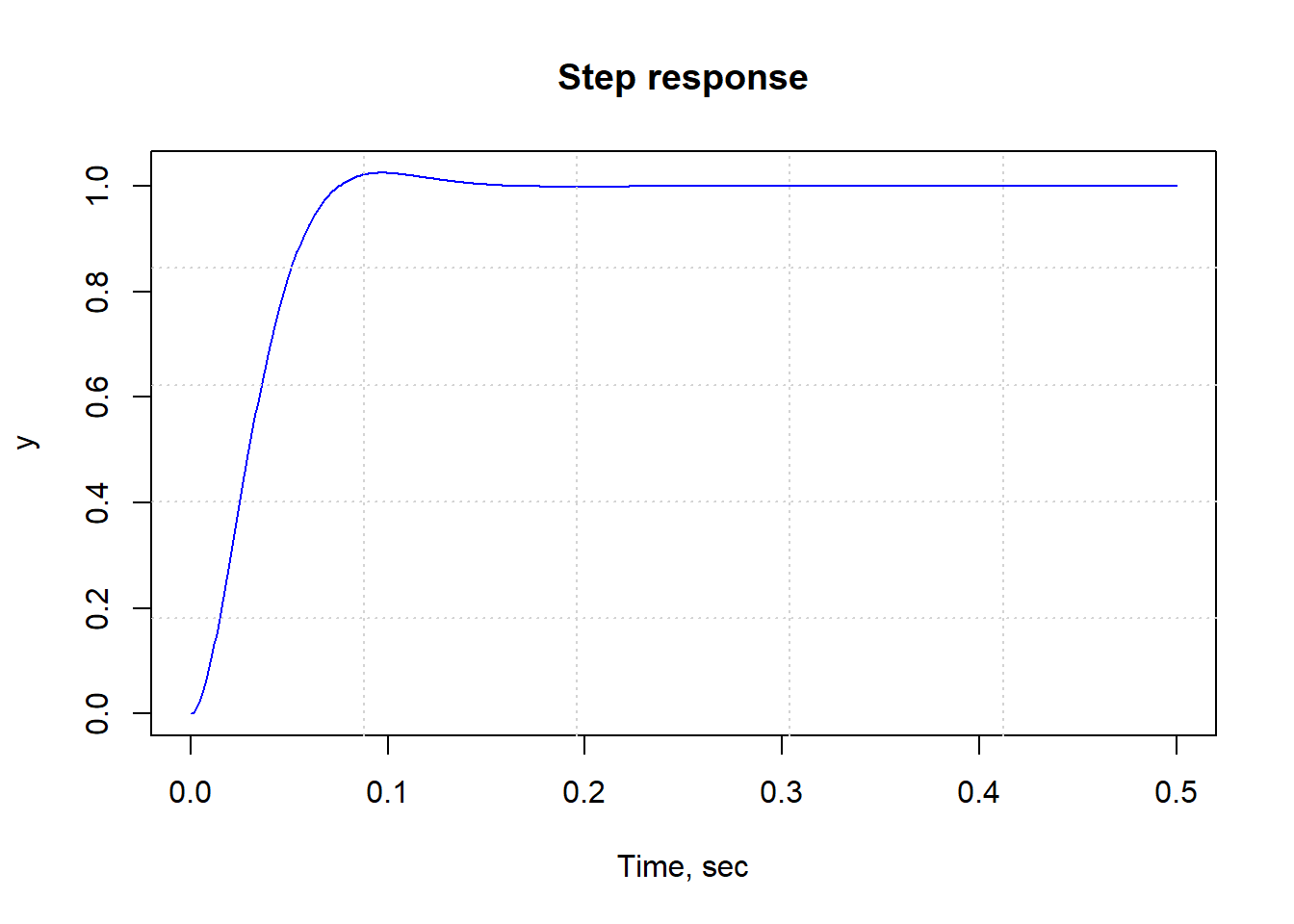 The closed-loop step response shows that the system is stable after adding a feedback controller. Then the spacecraft’s attitude is stabilized by the feedback controller.
The closed-loop step response shows that the system is stable after adding a feedback controller. Then the spacecraft’s attitude is stabilized by the feedback controller.
Conclusions
R is a suitable tool not only to explore the stability of a system but also to design a controller that will be able to stabilize the spacecraft. Most of the Aerospace Engineers use Matlab which is a software with lot of tools for spacecraft’s controller design in term of ploting the Bode diagram, ploting the compensated and uncompensated system, getting the gain margin and the phase margin,..but I am sure R is also a good tool and could perform some of the work we do in Aerospace using Matlab.
References
Ubah B. C., (2017), A Control System Toolbox, 0.2.5